알고리즘이란?
알고리즘이란 무엇일까?
"알고리즘이란 무엇일까?"라는 질문에 대한 답은 매우 중요하며, 컴퓨터 과학 및 수학과 같은 많은 분야에서 기본적인 요소로 작용합니다. 기본적으로, 알고리즘이란 주어진 문제를 해결하기 위한 명확하고 정확한 절차나 규칙의 집합을 의미합니다. 하지만 이 이해를 넘어, 이것은 또한 생각의 표현, 아이디어의 구현, 그리고 복잡성을 단순화하는 방법입니다.
알고리즘은 일련의 단계적인 지시사항입니다. 이는 컴퓨터 프로그래밍의 핵심 요소이며, 컴퓨터가 우리가 원하는 작업을 수행하도록 지시하는 방법입니다. 간단한 데이터 정렬에서부터 복잡한 인공지능 알고리즘까지, 모든 컴퓨터 프로그램은 기본적으로 알고리즘의 모음입니다.
알고리즘은 일상생활의 모든 측면에도 깊숙이 녹아있습니다. 예를 들어, 조리법은 재료를 특정한 결과물, 즉 완성된 요리로 변환하는 알고리즘입니다. 또는, 우리가 친구에게 집으로 오는 길을 설명할 때, 우리는 사실상 경로를 찾는 알고리즘을 제공하는 것입니다. 이런 방식으로 보면, 알고리즘은 명확한 결과를 달성하기 위한 단계별 지침의 집합입니다.
이 모든 것들을 통해, 알고리즘은 명확하고, 효과적이며, 실용적인 해결책을 제공하는 도구입니다. 알고리즘이란 단어는 그 자체로 간단해 보일지라도, 그것은 문제를 이해하고, 문제를 분석하며, 해결책을 찾아내는 데 필요한 강력한 생각의 도구를 나타냅니다. 알고리즘을 통해 우리는 복잡한 문제를 다루는 방법을 배우며, 이를 통해 우리는 더 나은 결정을 내리고, 더 효과적으로 문제를 해결할 수 있게 됩니다.
알고리즘의 특성
- 명확성: 모든 알고리즘은 단순하고 명확해야 합니다. 그 단계는 명확하게 정의되어야 하며, 모호성이 없어야 합니다. 각 단계는 특정한 연산을 수행하며, 이는 고유하고 잘 정의된 결과를 생성합니다. 이것은 알고리즘의 각 단계가 서로 분리되어 있으며, 각 단계가 명확하고 이해하기 쉬운 작업을 수행한다는 것을 의미합니다. 이것은 알고리즘을 이해하고 따르는 데 중요한 요소입니다.
- 유한성: 알고리즘은 유한한 단계 후에 종료되어야 합니다. 즉, 알고리즘은 반드시 언젠가는 완료되어야 합니다. 이는 알고리즘의 목표를 달성하거나 문제를 해결하는 데 필요한 단계의 수를 제한한다는 것을 의미합니다. 이것은 알고리즘이 결코 무한 루프에 빠지지 않으며, 항상 특정 조건이 충족되면 종료된다는 것을 보장합니다.
- 효과성: 알고리즘의 각 단계는 효과적이어야 합니다. 즉, 각 단계는 실행 가능하고, 해당 단계를 수행하는 데 필요한 시간과 리소스가 최소화되어야 합니다. 이것은 알고리즘의 성능을 최적화하는 데 중요하며, 이는 특히 대량의 데이터를 처리하거나 복잡한 계산을 수행해야 하는 경우에 중요합니다.
- 입력: 알고리즘은 하나 이상의 명확하게 정의된 입력을 가지고 있어야 합니다. 입력은 알고리즘의 작동에 필요한 데이터나 정보를 제공하며, 이는 알고리즘이 실행되는 동안 변환되거나 처리됩니다. 이러한 입력은 알고리즘의 동작을 이해하고 예측하는 데 필요한 통찰력을 제공합니다.
- 출력: 알고리즘은 최소 하나 이상의 명확하게 정의된 출력을 생성해야 합니다. 출력은 알고리즘의 실행 결과를 나타내며, 이는 일반적으로 입력에 대한 몇 가지 유용한 정보나 변환입니다. 이러한 출력은 알고리즘이 어떤 문제를 해결하거나 어떤 작업을 수행하는지를 이해하는 데 도움이 됩니다.
다양한 알고리즘
- 정렬 알고리즘: 이는 데이터를 특정 순서(일반적으로 숫자의 오름차순 또는 내림차순)에 따라 재배열하는 알고리즘입니다. 버블 정렬, 선택 정렬, 삽입 정렬, 퀵 정렬, 병합 정렬 등과 같은 다양한 정렬 알고리즘은 각기 다른 방법으로 데이터를 정렬하며, 각각의 알고리즘이 그 자체의 장점과 단점을 가지고 있습니다. 이러한 이해는 데이터를 빠르고 효율적으로 정렬해야 하는 다양한 상황에 대응하는 능력을 키웁니다.
- 탐색 알고리즘: 탐색 알고리즘은 데이터 구조 내에서 특정 항목을 찾는 데 사용됩니다. 이러한 알고리즘은 선형 탐색, 이진 탐색 등과 같은 다양한 방법을 사용하여 데이터를 탐색하고, 각 방법은 그 자체의 특징과 사용 사례를 가지고 있습니다. 이해와 활용력을 향상시키는 것은 데이터의 빠른 검색과 효율적인 관리를 가능하게 합니다.
- 동적 프로그래밍 알고리즘: 동적 프로그래밍은 복잡한 문제를 작은 하위 문제로 분할하고, 이 하위 문제의 해결책을 결합하여 원래 문제를 해결하는 방법입니다. 이는 피보나치 수열, 배낭 문제, 최장 공통 부분 문자열 등과 같은 다양한 문제에 적용할 수 있습니다. 동적 프로그래밍 알고리즘의 이해는 더욱 복잡한 문제를 효율적으로 해결하는 데 중요한 도구를 제공합니다.
문제를 잘 이해하고 분석하기
문제를 잘 이해하기
문제를 이해하는 과정은 사실상 모든 알고리즘 문제를 풀어나가는 데 필수적입니다. 이는 우리가 문제의 요구사항을 명확하게 파악하고, 필요한 알고리즘을 설계하고, 적절한 테스트 케이스를 생성하는 데 도움이 됩니다.
예를 들어, "정렬되지 않은 정수 배열이 주어졌을 때, 가장 빈번하게 등장하는 정수를 찾는 알고리즘을 작성하라."라는 문제를 생각해보세요. 이 문제를 해석하는 과정은 다음과 같습니다:
- 문제 이해하기: 첫 번째 단계는 문제를 읽고 이해하는 것입니다. 여기서 우리는 문제가 우리에게 어떤 것을 요구하는지 파악해야 합니다. 이 문제의 경우, 우리는 주어진 배열에서 가장 빈번하게 등장하는 정수를 찾아야 합니다.
- 요구사항 파악하기: 두 번째 단계는 문제의 요구사항을 파악하는 것입니다. 이 문제에서는 우리는 입력으로 정렬되지 않은 정수 배열을 받고, 그 배열에서 가장 빈번하게 등장하는 정수를 출력해야 합니다.
- 예외사항 파악하기: 세 번째 단계는 문제에서 확인할 수 있는 예외 케이스를 확인하는 것입니다. 실제 문제 설명에서 자세하게 설명되어 있는 경우도 있지만, 문제 설명을 통해 유추해야 하는 경우도 존재합니다. 정렬되지 않은 정수 배열이 주어졌을 때, 가장 빈번하게 등장하는 정수를 찾는 알고리즘을 작성하라의 경우에는 동일한 갯수의 정수가 2개 이상일 경우, 어떤 답을 반환해야 하는지가 예외 케이스가 될 수 있겠습니다.
이처럼, 문제 해석은 우리가 문제를 효과적으로 이해하고, 문제를 풀기 위한 알고리즘을 설계하고, 그 알고리즘이 정확하게 작동하는지 확인하는 데 도움이 되는 중요한 과정입니다. 이를 통해 우리는 문제의 해결 방안을 찾아내고, 이를 구체적인 코드로 변환하는 능력을 향상시킬 수 있습니다.
문제를 잘 분석하기
문제를 잘 분석하는 과정은 알고리즘 문제 해결의 가장 중요한 요소입니다. 문제를 분석하는 과정에서 우리는 문제의 복잡성을 파악하고, 가능한 해결책을 조사하며, 가장 적합한 알고리즘을 선택해 나가야 합니다.
문제를 분석하는 과정을 살펴보겠습니다.
- 문제를 작은 단위로 나누는 것은, 알고리즘 문제를 해결하는 데 매우 중요한 방법입니다. 이를 "분할 정복(Divide and Conquer)" 이라고도 합니다. 이 방법은 주어진 문제를 더 작고, 더 쉽게 해결할 수 있는 부분 문제로 나누는 것을 의미합니다. 이 작은 문제들을 각각 해결하고, 이들의 해결책을 합쳐서 원래의 문제를 해결하는 것이 분할 정복 전략의 핵심입니다. 이 방법은 문제를 보다 관리 가능한 부분으로 나누어 복잡성을 줄이는데 도움이 됩니다. 이는 문제 해결을 위한 논리적인 단계를 설정하는 데 도움이 되며, 이를 통해 문제의 각 부분에 대한 깊은 이해를 구축할 수 있습니다.
- 다음으로, 가능한 해결책을 조사합니다. 이 과정에서 우리는 다양한 알고리즘과 접근 방식을 고려하고, 그들의 장점과 단점을 비교합니다. 이러한 조사는 우리가 문제에 대한 깊은 이해를 갖게 하며, 가장 적합한 해결책을 찾아내는 데 도움이 됩니다.
- 마지막으로, 가장 적합한 알고리즘을 선택합니다. 여러 가지 가능한 해결책을 조사한 후, 우리는 문제를 가장 효과적으로 해결할 수 있는 알고리즘을 선택합니다. 이는 문제의 복잡성, 사용 가능한 리소스, 그리고 우리의 목표에 따라 달라집니다.
예를 들어, "두 개의 정렬된 배열이 주어졌을 때, 두 배열을 병합하여 하나의 정렬된 배열을 만드는 알고리즘을 작성하라"는 문제를 생각해 봅시다. 이 문제를 분석하면서 우리는 두 배열이 이미 정렬되어 있다는 사실을 이용해 효율적인 해결책을 찾을 수 있습니다. 우리는 두 배열의 첫 번째 원소를 비교하고, 더 작은 원소를 결과 배열에 추가하는 과정을 반복함으로써, 복잡성을 최소화하면서도 문제를 효과적으로 해결할 수 있는 알고리즘을 선택할 수 있습니다.
이처럼, 문제를 분석하는 과정은 우리가 알고리즘 문제 해결에 필요한 기본적인 도구를 갖추게 해줍니다. 이를 통해 우리는 문제에 대한 우리의 접근 방식을 개선하고, 더 효율적인 알고리즘을 설계하는 과정을 거치게 됩니다.
문제를 작은 단위로 분할하기
문제를 작은 단위로 분할하는 것은 복잡한 문제를 단순화하는 데 큰 도움이 됩니다. 이러한 접근 방식은 마치 하나의 복잡한 문제를 여러 개의 간단한 문제로 나누는 것과 비슷합니다. 각각의 작은 문제는 보다 쉽게 해결되며, 이를 하나씩 완료함으로써 전체 문제를 해결하는 과정을 단계별로 도달할 수 있습니다.
예를 들어, 다음과 같은 문제를 생각해 보겠습니다:
문제 1: "주어진 문자열에서 모든 대문자를 소문자로, 모든 소문자를 대문자로 바꾸고, 그 후 문자열을 거꾸로 배치하는 문제입니다."이 문제는 몇 가지 단계로 나눌 수 있습니다:
- 대소문자 변환: 주어진 문자열의 모든 문자를 순회하면서, 각 문자가 대문자인지 소문자인지 확인합니다. 대문자라면 소문자로, 소문자라면 대문자로 변환합니다. 이 단계는 각 문자에 대해 수행되므로, 작은 단위의 문제로 분할할 수 있습니다.
- 문자열 뒤집기: 대소문자가 변환된 문자열을 뒤집습니다. 문자열의 처음과 끝에서 시작하여, 각 위치의 문자를 서로 바꾸고, 중간 위치로 좁혀나가는 방식을 사용할 수 있습니다. 이 단계 역시 문자열의 각 위치에 대해 수행되므로, 작은 단위의 문제로 분할할 수 있습니다.
문제 2: 배열에서 최대값과 최소값 찾기 주어진 숫자 배열에서 최대값과 최소값을 찾는 알고리즘을 작성하는 문제입니다.
- 최대값 찾기: 배열의 첫 번째 원소를 최대값으로 가정하고, 배열을 순회하면서 각 원소가 현재 최대값보다 큰지 확인합니다. 더 큰 값이 발견되면, 그 값을 새로운 최대값으로 갱신합니다. 이 단계는 각 원소에 대해 수행되므로, 작은 단위의 문제로 분할할 수 있습니다.
- 최소값 찾기: 비슷하게, 배열의 첫 번째 원소를 최소값으로 가정하고, 배열을 순회하면서 각 원소가 현재 최소값보다 작은지 확인합니다. 더 작은 값이 발견되면, 그 값을 새로운 최소값으로 갱신합니다. 이 단계 역시 각 원소에 대해 수행되므로, 작은 단위의 문제로 분할할 수 있습니다.
문제 3: 피보나치 수열 계산하기 주어진 숫자 n에 대해 피보나치 수열의 n번째 항을 계산하는 알고리즘을 작성해야 합니다.
- 기본 케이스 확인: n이 0 또는 1인 경우에 대한 결과는 이미 알려져 있습니다. 이 경우들에 대한 결과를 반환합니다. 이는 작은 단위의 문제로 분할할 수 있습니다.
- 재귀적 계산: n이 1보다 큰 경우, 피보나치 수열의 n번째 항은 (n-1)번째 항과 (n-2)번째 항의 합입니다. 따라서 이 문제를 (n-1)번째 항과 (n-2)번째 항을 계산하는 두 개의 작은 단위의 문제로 분할할 수 있습니다.
이처럼 복잡한 문제도 작은 단위의 문제로 분할하면 각 부분을 독립적으로 해결할 수 있고, 이를 조합함으로써 전체 문제를 해결할 수 있습니다. 이 접근법은 문제 해결 과정을 단순화하고 구조화하는 데 큰 도움이 됩니다.
시간복잡도와 공간복잡도
알고리즘 문제를 풀다 보면 문제에 대한 해답을 찾는 것이 가장 중요합니다. 그러나 그에 못지않게, 효율적인 방법으로 문제를 해결했는지도 중요합니다. 혹시 문제를 풀다가, 이것보다 더 효율적인 방법은 없을까?, 또는 이게 제일 좋은 방법이 맞나?라는 생각을 해 본 적이 있나요? 효율적인 방법을 고민한다는 것은 시간 복잡도를 고민한다는 것과 같은 말입니다. 이번 챕터에서는 시간 복잡도와 Big-O(빅-오) 표기법에 대해서 배워 보도록 하겠습니다.
Big-O 표기법
시간 복잡도를 표기하는 방법은 다음과 같습니다.
- Big-O(빅-오)
- Big-Ω(빅-오메가)
- Big-θ(빅-세타)
위 세 가지 표기법은 시간 복잡도를 각각 최악, 최선, 중간(평균)의 경우에 대하여 나타내는 방법입니다. 이 중에서 Big-O 표기법이 가장 자주 사용됩니다. 빅오 표기법은 최악의 경우를 고려하므로, 프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려할 수 있기 때문입니다. "최소한 특정 시간 이상이 걸린다" 혹은 "이 정도 시간이 걸린다"를 고려하는 것보다 "이 정도 시간까지 걸릴 수 있다"를 고려해야 그에 맞는 대응이 가능합니다.
결과를 반환하는 데 최선의 경우 1초, 평균적으로 1분, 최악의 경우 1시간이 걸리는 알고리즘을 구현했고, 최선의 경우를 고려한다고 가정하겠습니다. 이 알고리즘을 100번 실행한다면, 최선의 경우 100초가 걸립니다. 만약 실제로 걸린 시간이 1시간을 훌쩍 넘겼다면, 어디에서 문제가 발생한 거지? 란 의문이 생길 겁니다. 최선의 경우만 고려하였으니, 어디에서 문제가 발생했는지 알아내기 위해서는 로직의 많은 부분을 파악해야 하므로 문제를 파악하는 데 많은 시간이 필요합니다.
평균값을 기대하는 시간 복잡도를 고려한다면 어떨까요? 알고리즘을 100번 실행할 때 100분의 시간이 소요된다고 생각했는데, 최악의 경우가 몇 개 발생하여 300분이 넘게 걸렸다면 최선의 경우를 고려한 것과 같은 고민을 하게 됩니다.
극단적인 예이지만, 위와 같이 최악의 경우가 발생하지 않기를 바라며 시간을 계산하는 것보다는 최악의 경우도 고려하여 대비하는 것이 바람직합니다. 따라서 다른 표기법보다 Big-O 표기법을 많이 사용합니다. 이어지는 내용에서, Big-O 표기법의 종류에 대해 알아보겠습니다.
O(1)
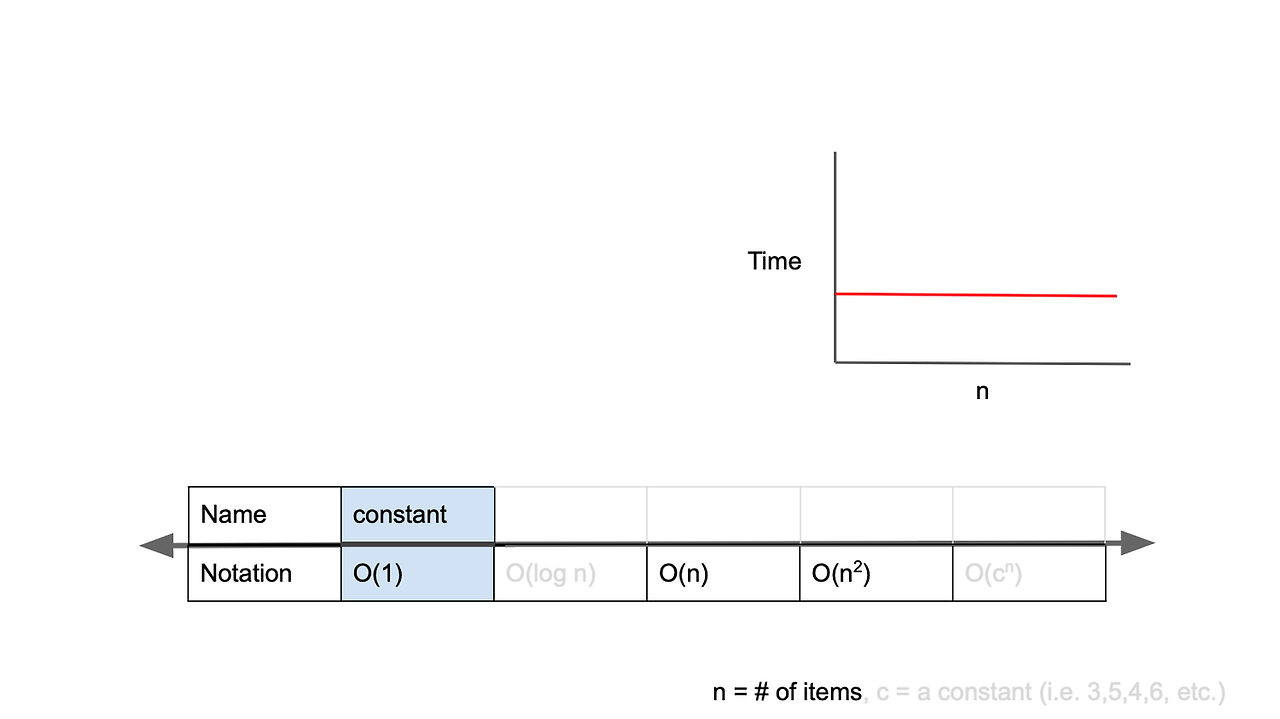
[그림] 시간 복잡도가 O(1)인 경우
Big-O 표기법은 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?를 표기하는 방법입니다. O(1)는 constant complexity라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않습니다. 다시 말해 입력값의 크기와 관계없이, 즉시 출력값을 얻어낼 수 있다는 의미입니다. O(1)의 시간 복잡도를 가진 알고리즘을 살펴보겠습니다.
public int O_1_algorithm(int[] arr, int index) { // Java로 구현한 코드
return arr[index];
}
def O_1_algorithm(arr, index): // Python으로 구현한 코드
return arr[index]
int O_1_algorithm(int arr[], int index) { // C, C++로 구현한 코드
return arr[index];
}
func O_1_algorithm(_ arr: [Int], _ index: Int) -> Int { // Swift로 구현한 코드
return arr[index]
}
fun O_1_algorithm(arr: IntArray, index: Int): Int { // Kotlin으로 구현한 코드
return arr[index]
}
[코드] O(1)의 시간 복잡도를 가지는 알고리즘 예시
위 알고리즘에선 입력값의 크기가 아무리 커져도 즉시 출력값을 얻어낼 수 있습니다. 예를 들어 arr의 길이가 100만이라도, 즉시 해당 index에 접근해 값을 반환할 수 있습니다.
O(n)
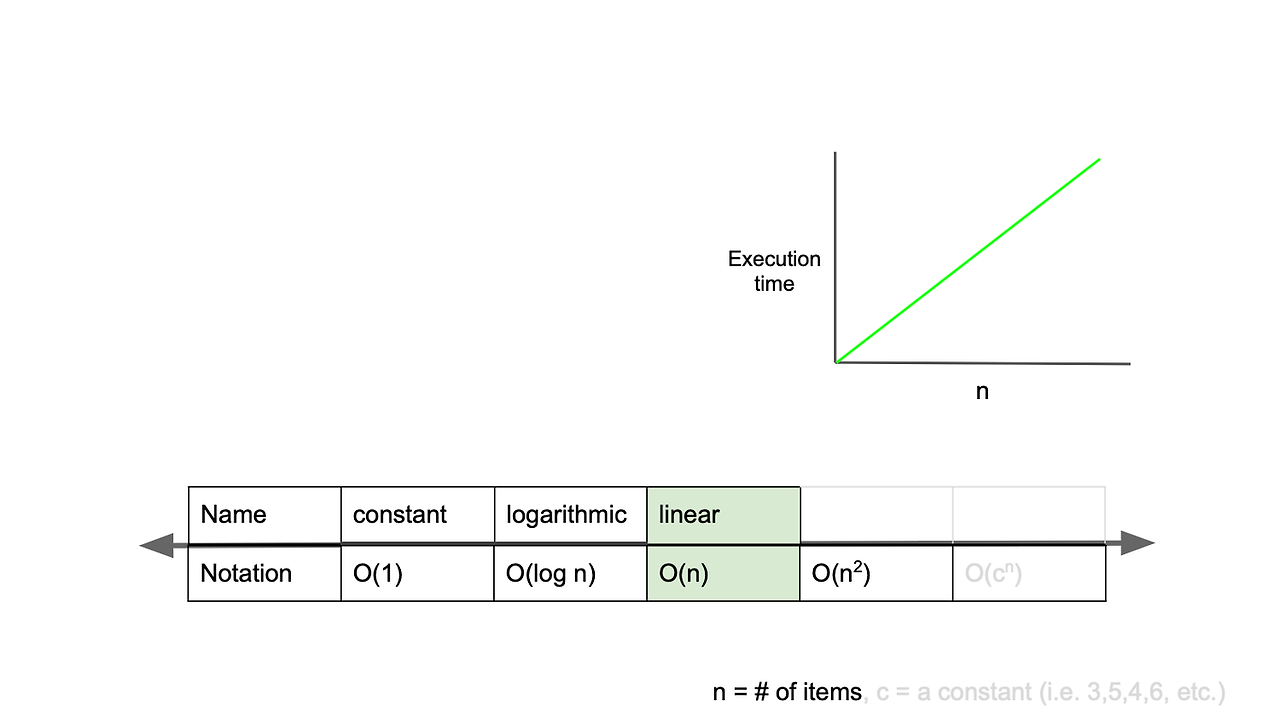
[그림] 시간 복잡도가 O(n)인 경우
O(n)은 linear complexity라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미합니다. 예를 들어 입력값이 1일 때 1초의 시간이 걸리고, 입력값을 100배로 증가시켰을 때 1초의 100배인 100초가 걸리는 알고리즘을 구현했다면, 그 알고리즘은 O(n)의 시간 복잡도를 가진다고 할 수 있습니다. O(n)의 시간 복잡도를 가진 알고리즘을 살펴보겠습니다.
public void O_n_algorithm(int n) { // Java로 구현한 코드
for(int i = 0; i < n; i++) {
// do something for 1 second
}
}
public void another_O_n_algorithm(int n) {
for(int i = 0; i < n * 2; i++) {
// do something for 1 second
}
}
def O_n_algorithm(n): // Python으로 구현한 코드
for i in range(n):
# do something for 1 second
pass
def another_O_n_algorithm(n):
for i in range(n * 2):
# do something for 1 second
pass
void O_n_algorithm(int n) { // C, C++로 구현한 코드
for(int i = 0; i < n; i++) {
// do something for 1 second
}
}
void another_O_n_algorithm(int n) {
for(int i = 0; i < n * 2; i++) {
// do something for 1 second
}
}
func O_n_algorithm(_ n: Int) { // Swift로 구현한 코드
for i in 0..<n {
// do something for 1 second
}
}
func another_O_n_algorithm(_ n: Int) {
for i in 0..<(n * 2) {
// do something for 1 second
}
}
fun O_n_algorithm(n: Int) { // Kotlin으로 구현한 코드
for (i in 0 until n) {
// do something for 1 second
}
}
fun another_O_n_algorithm(n: Int) {
for (i in 0 until (n * 2)) {
// do something for 1 second
}
}[코드] O(n)의 시간 복잡도를 가지는 알고리즘 예시
O_n_algorithm 함수에선 입력값(n)이 1 증가할 때마다 코드의 실행 시간이 1초씩 증가합니다. 즉 입력값이 증가함에 따라 같은 비율로 걸리는 시간이 늘어나고 있습니다. 그렇다면 함수 another_O_n_algorithm 은 어떨까요? 입력값이 1 증가할 때마다 코드의 실행 시간이 2초씩 증가합니다. 이것을 보고, "아! 그렇다면 이 알고리즘은 O(2n)이라고 표현하겠구나!"라고 생각할 수 있습니다. 그러나, 사실 이 알고리즘 또한 Big-O 표기법으로는 O(n)으로 표기합니다. 입력값이 커지면 커질수록 계수(n 앞에 있는 수)의 의미(영향력)가 점점 퇴색되기 때문에, 같은 비율로 증가하고 있다면 2배가 아닌 5배, 10배로 증가하더라도 O(n)으로 표기합니다.
O(log n)

[그림] 시간 복잡도가 O(log n)인 경우
O(log n)은 logarithmic complexity라고 부르며 Big-O표기법 중 O(1) 다음으로 빠른 시간 복잡도를 가집니다. 자료구조에서 학습하게 될 BST(Binary Search Tree)를 살펴보겠습니다. BST에선 원하는 값을 탐색할 때, 노드를 이동할 때마다 경우의 수가 절반으로 줄어듭니다. 이해하기 쉬운 게임으로 비유해 보자면 up & down을 예로 들 수 있습니다.
- 1~100 중 하나의 숫자를 플레이어1이 고른다 (30을 골랐다고 가정합니다).
- 50(가운데) 숫자를 제시하면 50보다 작으므로 down을 외친다.
- 1~50중의 하나의 숫자이므로 또다시 경우의 수를 절반으로 줄이기 위해 25를 제시한다.
- 25보다 크므로 up을 외친다.
- 경우의 수를 계속 절반으로 줄여나가며 정답을 찾는다.
매번 숫자를 제시할 때마다 경우의 수가 절반이 줄어들기 때문에 최악의 경우에도 7번이면 원하는 숫자를 찾아낼 수 있게 됩니다. BST의 값 탐색도 같은 로직으로 O(log n)의 시간 복잡도를 가진 알고리즘(탐색기법)입니다.
O(n^2)

[그림] 시간 복잡도가 O(n^2)인 경우
O(n^2)은 quadratic complexity라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미합니다.
예를 들어 입력값이 1일 경우 1초가 걸리던 알고리즘에 5라는 값을 주었더니 25초가 걸리게 된다면, 이 알고리즘의 시간 복잡도는 O(n^2)라고 표현합니다. O(n^2)의 시간 복잡도를 가진 알고리즘을 살펴보겠습니다.
public void O_quadratic_algorithm(int n) { // Java로 구현한 코드
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
// do something for 1 second
}
}
}
public void another_O_quadratic_algorithm(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
// do something for 1 second
}
for(int k = 0; k < n; k++) {
// do something for 1 second
}
for(int l = 0; l < n; l++) {
// do something for 1 second
}
}
}
}
def O_quadratic_algorithm(n): // Python으로 구현한 코드
for i in range(n):
for j in range(n):
# do something for 1 second
pass
def another_O_quadratic_algorithm(n):
for i in range(n):
for j in range(n):
# do something for 1 second
pass
for k in range(n):
# do something for 1 second
pass
for l in range(n):
# do something for 1 second
pass
void O_quadratic_algorithm(int n) { // C, C++로 구현한 코드
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
// do something for 1 second
}
}
}
void another_O_quadratic_algorithm(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
// do something for 1 second
}
for(int k = 0; k < n; k++) {
// do something for 1 second
}
for(int l = 0; l < n; l++) {
// do something for 1 second
}
}
}
func O_quadratic_algorithm(_ n: Int) { // Swift로 구현한 코드
for i in 0..<n {
for j in 0..<n {
// do something for 1 second
}
}
}
func another_O_quadratic_algorithm(_ n: Int) {
for i in 0..<n {
for j in 0..<n {
// do something for 1 second
}
for k in 0..<n {
// do something for 1 second
}
for l in 0..<n {
// do something for 1 second
}
}
}
fun O_quadratic_algorithm(n: Int) { // Kotlin으로 구현한 코드
for (i in 0 until n) {
for (j in 0 until n) {
// do something for 1 second
}
}
}
fun another_O_quadratic_algorithm(n: Int) {
for (i in 0 until n) {
for (j in 0 until n) {
// do something for 1 second
}
for (k in 0 until n) {
// do something for 1 second
}
for (l in 0 until n) {
// do something for 1 second
}
}
}[코드] O(n^2)의 시간 복잡도를 가지는 알고리즘 예시
2n, 5n을 모두 O(n)이라고 표현하는 것처럼, 3n^2, 5n^2도 n^2으로 표현합니다. n이 커지면 커질수록 지수가 주는 영향력이 점점 퇴색되기 때문에 이렇게 표기합니다.
O(2^n)

[그림] 시간 복잡도가 O(2^n)인 경우
O(2^n)은 exponential complexity라고 부르며 Big-O 표기법 중 가장 느린 시간 복잡도를 가집니다. 종이를 42번 접으면 그 두께가 지구에서 달까지의 거리보다 커진다는 이야기를 들어보신 적 있으신가요? 고작 42번 만에 얇은 종이가 그만한 두께를 가질 수 있는 것은, 매번 접힐 때마다 두께가 2배로 늘어나기 때문입니다. 구현한 알고리즘의 시간 복잡도가 O(2^n)이라면 다른 접근 방식을 고민해 보는 것이 좋습니다.
public int fibonacci(int n) { // Java로 구현한 코드
if(n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci (n - 2);
}
def fibonacci(n): // Python으로 구현한 코드
if n <= 1:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
int fibonacci(int n) { // C, C++로 구현한 코드
if(n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
func fibonacci(_ n: Int) -> Int { // Swift로 구현한 코드
if n <= 1 {
return 1
}
return fibonacci(n - 1) + fibonacci(n - 2)
}
fun fibonacci(n: Int): Int { // Kotlin으로 구현한 코드
if (n <= 1) {
return 1
}
return fibonacci(n - 1) + fibonacci(n - 2)
}[코드] O(2^n)의 시간 복잡도를 가지는 알고리즘 예시
재귀로 구현하는 피보나치 수열은 O(2^n)의 시간 복잡도를 가진 대표적인 알고리즘입니다. 브라우저 개발자 창에서 n을 40으로 두어도 수초가 걸리는 것을 확인할 수 있으며, n이 100 이상이면 평생 결과를 반환받지 못할 수도 있습니다.
공간 복잡도
공간 복잡도는 알고리즘이 실행되는 동안 필요한 메모리 공간의 양을 측정합니다. 역시 Big-O 표기법을 사용하여 표현되며, 알고리즘이 필요로 하는 추가적인 공간의 양을 나타냅니다. 일반적으로는 입력 크기에 따라 선형적으로 증가하는 경우가 많습니다. 예를 들어, 배열의 크기에 비례하여 추가 배열을 생성하는 경우가 이에 해당합니다.
최근에는 컴퓨터의 메모리 용량이 대폭 증가하면서 일반적인 문제 해결에 있어서 공간 복잡도는 크게 제약되지 않는 경우가 많습니다. 따라서, 대부분의 경우에는 시간 복잡도가 우선적으로 고려되고, 공간 복잡도는 상대적으로 중요성이 낮아졌습니다.
그러나 일부 특정한 상황에서는 공간 복잡도도 중요한 요소일 수 있습니다. 예를 들어, 다음과 같은 경우에 공간 복잡도에 대한 고려가 필요할 수 있습니다.
- 제한된 메모리 환경: 일부 임베디드 시스템이나 모바일 디바이스에서는 제한된 메모리 용량을 가지고 작동합니다. 이런 경우에는 공간 복잡도를 최소화하여 메모리를 효율적으로 사용해야 합니다.
- 대용량 데이터 처리: 대용량 데이터를 다루는 경우에는 메모리 사용이 중요한 문제가 될 수 있습니다. 예를 들어, 수십 GB 이상의 데이터를 메모리에 모두 로드할 수 없는 경우에는 데이터를 효율적으로 압축하거나 조각으로 나누어 처리해야 할 수도 있습니다.
- 재귀 알고리즘: 일부 재귀 알고리즘은 재귀 호출에 따라 스택 메모리를 많이 사용합니다. 따라서 재귀 알고리즘을 사용하는 경우에는 스택 오버플로우를 방지하기 위해 공간 복잡도를 고려해야 합니다.
또한, 메모리 사용량이 많은 경우에는 캐시 효율성과 같은 다른 요소에도 영향을 미칠 수 있으므로, 최적의 공간 사용 패턴을 고려하는 것이 중요합니다.
요약하자면, 대부분의 문제에서는 공간 복잡도를 크게 고려하지 않아도 되지만, 일부 특정한 상황에서는 메모리 제약과 효율성을 고려하여 공간 복잡도를 최적화하는 것이 필요할 수 있습니다.
시간 복잡도를 고려해야 하는 경우
일반적으로 코딩 테스트에서는 정확한 값을 제한된 시간 내에 반환하는 프로그램을 작성해야 합니다. 컴파일러 혹은 컴퓨터의 사양에 따라 차이는 있겠지만, 시간제한과 주어진 데이터 크기 제한에 따른 시간 복잡도를 어림잡아 예측해 보는 것은 중요합니다.
예를 들어 입력으로 주어지는 데이터에는 n만큼의 크기를 가지는 데이터가 있고, n이 1,000,000보다 작은 수일 때 O(n) 혹은 O(nlogn)의 시간 복잡도를 가지도록 예측하여 프로그램을 작성할 수 있습니다.
n^2의 시간 복잡도를 예측할 수 없는 이유는 실제 수를 대입해 계산해 보면 유추할 수 있습니다. 1,000,000^2은 즉시 처리하기에 무리가 있는 숫자입니다. (1,000,000 * 1,000,000 = 1,000,000,000,000) 만약 n ≤ 500으로 입력이 제한된 경우에는 O(n^3)의 시간 복잡도를 가질 수 있다고 예측할 수 있습니다. O(n^3)의 시간 복잡도를 가지는 프로그램을 작성한다면 문제를 금방 풀 수 있을 텐데, 시간 복잡도를 O(log n)까지 줄이기 위해 끙끙댈 필요는 없습니다.
따라서, 입력 데이터가 클 때는 O(n) 혹은 O(log n)의 시간 복잡도를 만족할 수 있도록 예측해서 문제를 풀어야 합니다. 그리고 주어진 데이터가 작을 때는 시간 복잡도가 크더라도 문제를 풀어내는 것에 집중하세요.
재귀(Recursion)
개념 및 작동 방식
재귀의 개념
재귀란 무엇일까요? 표준국어대사전에서는 이렇게 설명하고 있습니다.
재귀(再歸) : 원래의 자리로 되돌아가거나 되돌아옴.
재귀를 시각적으로 표현하면, 계속해서 원래의 상태로 돌아오는 아래의 이미지와 같습니다.

[그림] 재귀의 이미지 예시
이러한 정의와 예시를 바탕으로, 재귀를 코드로 표현하면 아래와 같이 작성할 수 있습니다.
public void recursion() {
System.out.println("This is");
System.out.println("recursion!");
recursion();
}[코드 1-1] Java로 표현한 재귀의 코드 예시
def recursion():
print("This is")
print("recursion!")
recursion()[코드 1-2] Python으로 표현한 재귀의 코드 예시
이 메서드를 호출하면 어떻게 될까요?

[그림 1-1] recursion 메서드의 호출 결과
recursion 함수(메서드)를 실행하면, 이 함수는 자신을 끝없이 호출하며 동일한 코드가 계속 실행되는 것을 확인할 수 있습니다. 이렇게 자신을 호출하는 함수를 재귀 함수라고 부릅니다. 재귀 함수를 효과적으로 사용하면 반복적인 작업을 수행해야 하는 문제를 더욱 간결한 코드로 해결할 수 있습니다.
재귀의 작동 방식
재귀 함수는 기본 조건(base case)과 재귀 호출(recursive call) 두 가지 요소로 구성됩니다. 기본 조건은 재귀 호출을 중단하는 조건이며, 재귀 호출은 주어진 문제를 더 작은 하위 문제로 분해하여 해결하는 데 사용됩니다.
재귀 함수의 작동 방식은 아래와 같습니다:
- 재귀 함수가 호출되면, 호출 스택(Call Stack)에 해당 함수의 정보가 저장됩니다. 이 정보에는 함수의 인자, 반환 주소, 지역 변수 등이 포함됩니다.
- 재귀 함수는 호출 스택에 저장된 정보를 사용하여 문제를 해결하거나 하위 문제를 생성합니다.
- 재귀 함수는 자신을 호출하여 이 하위 문제를 처리합니다. 이때, 원래의 문제보다 작은 하위 문제를 해결하기 위해 재귀 호출이 이루어집니다.
- 재귀 호출이 계속되면, 하위 문제들은 재귀적으로 처리되고, 기본 조건에 도달하면 재귀 호출이 중단됩니다.
- 재귀 호출이 중단되면, 호출 스택의 맨 위에 있는 함수가 반환됩니다. 이때, 반환된 값은 하위 문제의 해결에 따라 결정됩니다.
- 호출 스택의 상위 함수들이 차례대로 반환되며, 최종적으로 재귀 함수는 완전히 종료됩니다.
재귀 함수는 문제를 더 작은 하위 문제로 나누어 해결하며, 이 하위 문제의 결과를 결합하여 원래의 문제를 해결하는 방식을 사용합니다. 재귀 함수를 구현할 때는 적절한 기본 조건을 설정하여 재귀 호출이 무한히 반복되는 것을 방지해야 합니다. 또한, 재귀 함수의 호출 스택 크기에 주의하여 스택 오버플로우를 예방해야 합니다.
재귀적 문제 해결과 재귀 호출의 예시
재귀적 문제 해결이란?
재귀적 문제 해결(Recursive Problem Solving)은 문제를 더 작은 하위 문제로 나누어 해결하는 방식을 말합니다. 이 방법은 재귀 호출을 활용하여 주어진 문제를 더 작은 부분 문제로 분해하고, 이 하위 문제들의 해결 방법을 결합하여 원래의 문제를 해결합니다.
재귀적 문제 해결은 다음과 같은 단계로 진행됩니다:
- 기본 조건(Base Case) 설정:
- 재귀 호출을 중단할 수 있는 기본 조건을 설정합니다.
- 기본 조건은 문제의 크기가 충분히 작아져서 직접적으로 해결 가능한 상황을 의미합니다.
- 기본 조건이 충족되면 재귀 호출을 중단하고, 그에 따른 값을 반환합니다.
- 재귀 호출(Recursive Call):
- 주어진 문제를 더 작은 하위 문제로 분해하기 위해 함수가 자신을 호출합니다.
- 하위 문제의 크기는 원래 문제의 크기보다 작아야 합니다.
- 재귀 호출을 통해 하위 문제를 해결하고 그 결과를 반환받습니다.
- 하위 문제 해결과 결합:
- 재귀 호출을 통해 얻은 하위 문제의 해결책을 결합하여 원래 문제의 해결책을 도출합니다.
- 하위 문제의 해결책을 결합하는 방법은 문제에 따라 다를 수 있습니다. 일반적으로는 각 하위 문제의 해결책을 더하거나, 해결책 중 특정 조건을 만족한 해결책만 취합합니다.
- 재귀 호출의 종료와 결과 반환:
- 재귀 호출은 기본 조건이 충족될 때까지 계속되며, 기본 조건이 충족되면 재귀 호출이 중단됩니다.
- 재귀 호출의 종료 시점에 최종 결과를 반환합니다.
재귀적 문제 해결은 문제를 더 작은 단위로 나누어 해결하고, 하위 문제의 해결책을 결합하여 전체 문제의 해결책을 도출하는 방식입니다. 이 방식은 문제를 보다 직관적이고 간결하게 해결할 수 있는 장점이 있으며, 분할 정복(Divide and Conquer) 알고리즘과 잘 결합되어 다양한 문제에 적용될 수 있습니다.
코드로 확인하는 재귀 호출의 예시
1. 팩토리얼 계산:
팩토리얼은 자연수 n에 대해 n! = n * (n-1) * (n-2) * ... * 2 * 1을 의미합니다. 이 문제는 재귀적으로 해결할 수 있습니다. n!은 n * (n-1)!로 표현될 수 있으므로, 재귀 호출을 활용하여 팩토리얼을 계산할 수 있습니다.
def factorial(n):
if n == 0:# 기본 조건: 0!은 1로 정의됩니다.return 1
else:
return n * factorial(n-1)# 재귀 호출: n! = n * (n-1)![코드 1-1] Python으로 구현한 팩토리얼
public static int factorial(int n) {
if (n == 0) {
return 1;// 기본 조건: 0!은 1로 정의됩니다.
} else {
return n * factorial(n - 1);// 재귀 호출: n! = n * (n-1)!
}
}[코드 1-2] Java로 구현한 팩토리얼
위 코드에서 n은 계산하려는 팩토리얼의 값입니다. 함수 내부에서 재귀 호출을 활용하여 n과 factorial(n-1)의 곱으로 팩토리얼을 계산합니다.
함수의 작동 원리는 아래와 같습니다:
- 입력값 n이 0인 경우, 팩토리얼의 정의에 따라 1을 반환합니다. 이 부분이 재귀 함수의 기본 조건(base case)입니다.
- 입력값 n이 0이 아닌 경우, n과 factorial(n-1)의 곱으로 팩토리얼을 계산하기 위해 재귀 호출을 수행합니다. 함수 내부에서 n * factorial(n-1)을 반환합니다.
- 재귀 호출은 n이 0이 될 때까지 계속되며, 호출 스택에 재귀 함수가 쌓이게 됩니다.
- 재귀 호출이 종료되면 호출 스택의 맨 위에 있는 함수가 반환되면서 팩토리얼 값이 계산됩니다.
이제 함수를 호출하여 팩토리얼 값을 계산할 수 있습니다. 예를 들어, factorial(5)를 호출하면 5!인 120이 반환됩니다. 재귀 호출을 통해 팩토리얼을 계산하는 이 방식은 문제를 더 작은 하위 문제로 분해하여 해결하는 재귀적 접근 방법을 잘 보여줍니다.
2. 피보나치 수열:
피보나치 수열은 이전 두 수의 합으로 구성되는 수열입니다. n번째 피보나치 수를 구하기 위해 n-1번째와 n-2번째 피보나치 수를 더하는 재귀 호출을 사용할 수 있습니다.
def fibonacci(n):
if n <= 1:# 기본 조건: n이 0 또는 1인 경우에는 n을 반환합니다.return n
else:
return fibonacci(n-1) + fibonacci(n-2)# 재귀 호출: n번째 피보나치 수 = (n-1)번째 피보나치 수 + (n-2)번째 피보나치 수[코드 2-1] Python으로 구현한 피보나치
public static int fibonacci(int n) {
if (n <= 1) {// 기본 조건: n이 0 또는 1인 경우에는 n을 반환합니다.return n;
} else {// 재귀 호출: n번째 피보나치 수 = (n-1)번째 피보나치 수 + (n-2)번째 피보나치 수return fibonacci(n - 1) + fibonacci(n - 2);
}
}[코드 2-2] Java로 구현한 피보나치
위 코드에서 n은 계산하려는 피보나치 수열의 위치입니다. 함수 내부에서는 재귀 호출을 활용하여 n-1번째와 n-2번째 피보나치 수를 더하여 n번째 피보나치 수를 계산합니다.
함수의 작동 원리는 아래와 같습니다:
- 입력값 n이 0 또는 1인 경우, 해당 위치의 값이 그대로 피보나치 수열의 값이므로 n을 반환합니다. 이 부분이 재귀 함수의 기본 조건(base case)입니다. (수열의 위치는 0번부터 시작합니다.)
- 입력값 n이 0 또는 1이 아닌 경우, n-1번째와 n-2번째 피보나치 수를 재귀 호출을 통해 계산합니다. fibonacci(n-1) + fibonacci(n-2)를 반환합니다.
- 재귀 호출은 n이 0 또는 1이 될 때까지 계속되며, 호출 스택에 재귀 함수가 쌓이게 됩니다.
- 재귀 호출이 종료되면 호출 스택의 맨 위에 있는 함수가 반환되면서 피보나치 수열의 값이 계산됩니다.
이제 함수를 호출하여 피보나치 수열의 특정 위치의 값을 계산할 수 있습니다. 예를 들어, fibonacci(6)을 호출하면 6번째 피보나치 수인 8이 반환됩니다. 재귀 호출을 통해 피보나치 수열을 계산하는 이 방식은 문제를 더 작은 하위 문제로 분해하여 해결하는 재귀적 접근 방법을 잘 보여줍니다.
재귀 알고리즘의 시간복잡도와 공간복잡도
재귀 함수의 시간복잡도
재귀 함수의 시간복잡도를 계산하려면 재귀 호출의 횟수와 각 재귀 호출에서 소요되는 시간복잡도를 고려해야 합니다. 일반적으로 재귀 호출의 횟수는 하위 문제의 개수와 유사하거나 약간 작은 경우가 많으므로, 하위 문제의 개수에 따라 재귀 함수의 시간복잡도가 결정됩니다.
재귀 함수의 시간복잡도를 계산하는 과정은 다음과 같습니다:
- 재귀 호출의 횟수 파악:
- 재귀 함수가 몇 번 호출되는지 파악합니다.
- 재귀 호출의 횟수는 대체로 입력값에 따라 결정됩니다. 예를 들어 팩토리얼 구현 코드에서 입력값이 n인 경우, 재귀 함수가 n번 호출될 수 있습니다.
- 각 재귀 호출에서의 시간복잡도 분석:
- 재귀 함수 내에서 수행되는 연산이나 루프 등의 작업을 고려하여 각 재귀 호출에서의 시간복잡도를 계산합니다.
- 팩토리얼과 피보나치 구현 코드 모두 한 번의 호출에서의 시간복잡도는 O(1)입니다. 재귀 호출을 제외하면 추가적인 반복 작업이 없기 때문입니다.
- 재귀 호출의 횟수와 각 재귀 호출에서의 시간복잡도 곱하기:
- 재귀 호출의 횟수와 각 재귀 호출에서의 시간복잡도를 곱합니다.
- 재귀 호출의 횟수는 주로 하위 문제의 개수와 유사하거나 약간 작은 값이기 때문에 하위 문제의 개수에 따라 재귀 함수의 시간복잡도가 결정됩니다.
- 팩토리얼 구현의 경우, factorial(5)일 경우 5, 4, 3, 2, 1까지 호출되고 탈출하기 때문에 5번 호출로 입력된 n = 5, 즉 O(n)입니다.
- 그러나, 재귀 호출에서 반복적인 계산이 발생하는 경우 시간복잡도가 더 증가할 수 있습니다.
- 피보나치 수열 구현의 경우를 살펴보겠습니다.
fibonacci(5) -> fibonacci(4) + fibonacci(3) -> fibonacci(3) + fibonacci(2) -> fibonacci(2) + fibonacci(1) -> fibonacci(1) -> fibonacci(2) + fibonacci(1) -> fibonacci(1)- 중복 호출이 발생하여 fibonacci(3)이나 fibonacci(2)와 같은 하위 문제가 반복적으로 계산됩니다. 이로 인해 재귀 호출의 횟수는 입력값 n에 대해 2^n으로 지수적으로 증가하게 됩니다.
- 시간복잡도 분석 결과 도출:
- 재귀 호출의 횟수와 각 재귀 호출에서의 시간복잡도를 곱한 값을 최종적인 시간복잡도로 도출합니다.
- 일반적으로 재귀 호출의 횟수에 따라 시간복잡도가 결정되므로, 하위 문제의 개수를 고려하여 재귀 함수의 시간복잡도를 분석합니다.
재귀 함수의 시간복잡도 계산은 재귀 호출의 횟수와 각 재귀 호출에서의 시간복잡도를 고려하여 분석하는 과정입니다. 이를 통해 재귀 함수의 성능과 시간복잡도를 정량적으로 평가할 수 있습니다.
재귀 함수의 공간복잡도
재귀 함수의 공간복잡도를 계산하려면 재귀 호출 시 사용되는 추가적인 메모리 공간을 고려해야 합니다. 주로 호출 스택(Call Stack)이라는 공간을 사용하여 재귀 함수의 실행 상태를 저장합니다.
재귀 함수의 공간복잡도를 계산하는 과정은 다음과 같습니다:
- 재귀 호출의 깊이 파악:
- 재귀 함수가 몇 단계까지 호출되는지 파악합니다.
- 재귀 호출의 깊이는 대체로 입력값에 따라 결정됩니다. 예를 들어, 입력값이 n인 경우, 팩토리얼 구현의 경우 재귀 함수의 깊이는 n까지 증가할 수 있습니다.
- 호출 스택의 사용 공간 분석:
- 재귀 호출 시 호출 스택에 저장되는 데이터의 크기를 분석합니다.
- 호출 스택에는 재귀 호출 시 필요한 매개변수, 지역 변수, 복귀 주소 등의 정보가 저장됩니다.
- 재귀 호출의 깊이에 따라 호출 스택의 크기가 증가하게 되므로, 재귀 호출 시 사용되는 추가적인 메모리 공간을 고려해야 합니다.
- 호출 스택의 최대 크기 계산:
- 재귀 호출의 깊이에 따라 호출 스택의 크기가 결정됩니다.
- 재귀 호출이 깊어질수록 호출 스택의 크기도 증가하게 되므로, 재귀 호출의 깊이에 따른 호출 스택의 최대 크기를 계산합니다.
- 공간복잡도 분석 결과 도출:
- 호출 스택의 최대 크기를 기반으로 재귀 함수의 공간복잡도를 도출합니다.
- 호출 스택의 크기는 재귀 호출의 깊이에 비례하므로, 재귀 함수의 공간복잡도는 재귀 호출의 깊이에 비례하게 됩니다.
재귀 함수의 공간복잡도 계산은 재귀 호출 시 사용되는 추가적인 메모리 공간을 고려하여 분석하는 과정입니다. 이를 통해 재귀 함수의 메모리 사용량과 공간복잡도를 정량적으로 평가할 수 있습니다.
